

The next number you will be dividing by is 47. It says that if you divide a polynomial, f(x), by a linear expression, x-A, the remainder will be the same as f(A). Just as you did the first time, simply write a small 4 above and to the right of the number 4. By clicking Accept all cookies, you agree Stack Exchange can store cookies on your device and disclose information in accordance with our Cookie Policy.
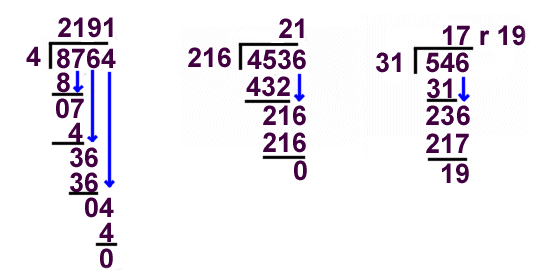
In addition, they are often interested in what does the remainder mean in polynomial long division? Division equation in latex closed Ask Question Asked 7 years, 9 months ago. It should be noted that the remainder theorem only works when a function is divided by a linear polynomial, which is of the form x + number or x - number. The remainder theorem states that when a polynomial, f(x), is divided by a linear polynomial, x - a, the remainder of that division will be equivalent to f(a). With allowance for this, what does the remainder tell you? In arithmetic, the remainder is the integer "left over" after dividing one integer by another to produce an integer quotient (integer division). In mathematics, the remainder is the amount "left over" after performing some computation. Adding to that, what is the remainder used for? When your division ends with a remainder, you must make sure that your remainder is less than your divisor. A part of basic arithmetic, long division is a method of solving and finding the answer and remainder for division problems that involve numbers with at least two digits. After you have your remainder, you write it on top of the division bar, with an r in front of it, like this: 25 r 3.


 0 kommentar(er)
0 kommentar(er)
